Records
While records are quite common in other programming languages, A record in F# is similar to a struct in C / C++; here is how to make one:
type Point = {x:int; y:int}
Here, we declare a new Point type that has two fields, x and y. The great thing now is that in F#, any structure you create that matches this pattern will automatically be a Point! For instance:
let p1 = {x1=11; y1=12}
This is automatically a Point, despite the fact that you never explicitly declare it as one. You can confirm this by typing it in the interpreter. You can access these fields as you’d expect with p1.x1 and p1.y1 but F# has a better way:
let {x=x1; y=y1} = p1
This will assign the x field of p1 to x1 and the y field of p1 to y1. You could use this as part of a function, for example:
let sum_coords {x=x1; y=y1} =
x1 + y1
This function takes a point, and sums its x and y ordinates.
Discriminated Unions
Discriminated Unions are something you will only find in functional languages. They are an great way to define complex types that combine multiple other types.
For instance, you might define a Colour type as follows:
type Colour =
| Red
| Green
| Blue
| Other of string
Here, we are defining Colour as a new type that can either be Red, Green, Blue, or Other. In case it is Other we can provide our own value. All of the following are of type Colour:
let g = Green
let cyan = Other “cyan”
Let’s make this Colour type more interesting by allowing for combinations of colours:
type Colour =
| Red
| Green
| Blue
| Other of string
| Combination of Colour * Colour
With the above we can define colours as:
let colour1 = Combination(Red, Blue)
let colour2 = Combination(colour1, Green)
The Colour * Colour above allows use to make a pair of Colours, as you can see, we have a recursive type here where a colour can be a combination of colours!
We’ll look at one final example, that of a simple mathematical expression involving integers:
type Expression =
| Number of int
| Sum of Expression * Expression
| Product of Expression * Expression
Here the ‘*’ does not mean product, but instead it signifies a combination or a tuple. What the above code means is that an Expression is a type of data that can one of be:
• An integer Number
• A Sum of two Expressions
• The Product of two Expressions
As you can see, this definition is recursive. So an Expression be a Product that is a combination of a Sum Expression and a Number Expression. The Sum in turn is a combination of two Number expressions. You can see this in action below:
let exp1 = Sum(Number 1, Number 3)
let exp2 = Product(exp1, Number 4)
In the above code exp2 is equivalent to: Product (Sum (Number
1,Number 3),Number 4)
Now you might be wondering how to use these Unions, and that happens to bring us to one of the most powerful features of F#, pattern matching. We’ll see how we can use patten matching to evaluate this above expression.
Pattern Matching
There is a good reason why we haven’t looked at even the basic ifthen- else syntax for F#, and that is because a much better alternative is available via pattern matching. Pattern matching allows you to branch code paths based on the value encountered, and this matching can look into the data structures themselves to make such a match. Think of it like switch case on steroids.
Let’s look at an example where we want a function to return the string “one” if it is provided the integer 1 and to return the string “many” otherwise. Normally you’d use an if-then clause here, but we have something better:
let oneOrMany x =
match x with
| 1 -> “one”
| _ -> “many”
If you were to now run oneOrMany 2 the function would return “many”. Each branch above handles one case, and here we have two. The first one matches x with 1 while the second one _ is a wildcard that matches all other cases.
Now imagine if we had to have three cases, the first where x is 1, the second where it is less than 10 and the third where it is 10 or more. If you’re worried that we’d have to write a separate case for all numbers from 2 to 9, don’t worry F# has something better:
let one FewMany x =
match x with
| 1 -> “one”
| a when a < 10 -> “few”
| _ -> “many”
It is also possible to have patterns like | 2 | 3 | 4 to match all those cases in one branch. Pattern matching can even look inside records, lists and Unions. Let’s quickly look at how matching records is done in F# :
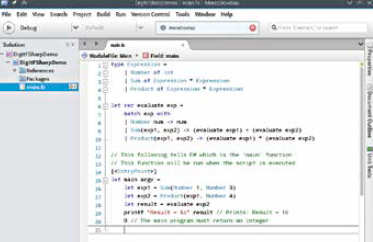
MonoDevelop on Linux being used to develop our expression evaluator.
let quadrant p =
match p with
| { x = x1; y = y1 } when x1 >= 0 && y1 >= 0 -> “I”
| { x = x1; y = y1 } when x1 < 0 && y1 >= 0 -> “II”
| { x = x1; y = y1 } when x1 < 0 && y1 < 0 -> “III”
| { x = x1; y = y1 } when x1 >= 0 && y1 < 0 -> “IV”
| _ -> “?”
Here p is a Point as defined above in the section on Records. This function will look at the ordinates of the Point p and return which quadrant it’s in. If you wanted to match points where x is 2 and y can be anything, you could match it as | { x = x1; y = _} -> doSomething. Now let’s do something really exciting, let’s write a function that
will evaluate our Expression type as defined in the previous section. You’ll find that the function is surprisingly concise:
let rec evaluate exp =
match exp with
| Number num -> num
| Sum(exp1, exp2) -> (evaluate exp1) + (evaluate exp2)
| Product(exp1, exp2) -> (evaluate exp1) * (evaluate exp2)
Now try using this function on the expressions we created in the previous section and you will find that it works! Note also that this function is being declared as let rec instead of just let as with other functions, the rec here is to tell F# that the function is recursive and as such should be able to call itself.
The above code just makes sense when you think about it, because that is how you would logically solve any expression.
Conclusion
There is still so much more to F# that we can’t go into in this article, but hopefully you have enough of a taste to get you excited about it! Just to give you a taste of some things you are missing out on, in F# you can create measurement units such as cm, m, inch, foot etc, to ensure that you can’t add cms and inches. You can avoid
null pointer exceptions by using optional types, and threading and asynchronous operations are built-in. We haven’t even looked at arrays and lists here and both of those are an important part of any language, and they have some special syntax when it comes to F#. As we’ve mentioned before, F# is a .NET language, so it already has the reach and capability of the .NET platform. If you are already engaged with that ecosystem, F# is well worth trying out.