Solving a Constraint Program by Hand:
In chess, the queen has the widest range of motion. It can move any number of spaces horizontally, vertically, and diagonally in any direction. So placing them such that no queen can attack any other one requires quite a bit of strategy. Given this problem, we need to figure out what should be the variables, and what should be the constraints. Before we dive into solving this using a computer, let’s take a simple version of this problem and see how one could solve it by hand. We’ll look at a 4×4 problem since there is no solution possible for 2×2 and 3×3 boards — think about it and you’ll see why.
First of all, we can immediately see a constraint. No two queens can be on the same row, or the same column. So we’ll take our 4 queens, and assign each its own column. Now we just need to figure out which row each should be on. Let’s start by putting the first queen in the first possible location, the top-left corner. This eliminates all spaces on the same row, column and diagonal. For the second queen, we have two options on the second column so let’s put it in the first one for now and move on. The second we do this, we realise that this won’t work. We have eliminated all spaces in the third column.
At this point, we need to backtrack. We now know that if the first queen is where it is, the second one can’t be in this location. Let’s move it to the next possible location at row 4. And, let’s stop right here. We can see two free spaces, and both are diagonal to each other. This will never work. What have we gotten ourselves into? Right?!
We have eliminated both possible locations for the second queen, from this we can conclude that the first queen is misplaced. At this point, we need to go back two steps, and move the first queen to another location, the second row. On doing this, we immediately see that there is only one spot in the second column, so let’s place one there as well.
This in turn leaves only one spot for the third queen in the first row. This now leaves one space for our final queen. And so ladies and gentlemen, we finally have a solution.
Now let’s do this for 10 queens. Just kidding! Let’s look at a possible constraint programming solution that works for any number of queens. The program we will build below can give you a solution for as many as 30 queens in under a second.
Building a Constraint Program:
At first glance, you might think that each queen will need two variables, a row, and a column. Certainly it is possible to develop a solution that way. We have already discovered above though, that each queen will be in a different column. So why not just assign one to each? Queen 1 in column 1, and so on. We can even use an array for this where the index can be the column number and the row can be the value of the array at that index.
The first constraint we can place now is that all the queens are in different rows. We have done this before when we wanted all letters in the “SEND+MORE=MONEY” problem to be distinct, we use the alldifferent command. Next comes the tricky part, how do we convey that no two queens should be along the same diagonal? A few smart people have discovered the trick to this, and it is quite clever when you see how it works.
The solution is to use two constraints, the first constraint is that no two queens can have the value of row number + column number the same; and the second constraint is that no two queens can have their row number – column number of the same value.
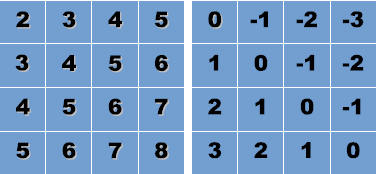
This might seem counter-intuitive to you, so we have attached an illustration that shows a 4×4 matrix where each cell has the sum row + column number in it; and another matrix that shows the difference row – column number. You’ll see that two cells having the same value corresponds to them being along the same diagonal. Here is the final code from the MiniZinc sample set with comments and the output procedure removed for brevity:
int: n;
array [1..n] of var 1..n: q;
include “alldifferent.mzn”;
constraint alldifferent(q);
constraint alldifferent([ q[i] + i | i in 1..n]);
constraint alldifferent([ q[i] – i | i in 1..n]);
solve :: int_search(q, first_fail, indomain_min, complete)
satisfy;
The above tables illustrate how sum of row and column number (left) and their difference (right) vary.
The final solve line in the code above is actually quite magical. The parameters provided there can be the difference between a solution derived in seconds, or in hours, or even not at all. Let’s see what they do then. First of all, int_search as you may guess from the name, searches for integer values within q. The first_fail parameter is interesting as it tells the compiler to first try the solutions that have a greater chance of failing first. In context to the n-Queens program, the solver will try to place a queen in the column with the fewest free spaces. This way, if it fails, it will quickly backtrack rather than going down the wrong path for longer. The third option – indomain_min instructs the compiler to start with the lowest row number (like we did in the manual solution above). Finally, the complete parameter makes the program look for all possible combinations till it finds a solution.
As you can see, while the solution is short, sweet and fast, it takes considerable understanding of the solution to model the problem in a way that can lead to a solution. Like any programming language, this is an intuition that the programmer needs to develop, as constraint programming has no shortcuts.
Conclusion:
Constraint programming is an exciting paradigm of computing, one that many people don’t come across soon enough. As you might have guessed from the above article though, it is quite powerful when applied correctly.
You might also be able to understand why it is not more commonly used. It isn’t really something you can write an entire software package in. For some kind of problems though, it can be the perfect tool for the job.
The good news here is that, you don’t need to use a pure constraint programming language to take advantage of this paradigm. For one, it is possible to embed such programs within traditional software so the constraint programming bits can be written in their native language.
For instance, you could build a Sudoku solver that combines a Python / Java / C++ program for the UI with a constraint programming at the back end that actually solves the problem.
The popular ECLiPSe Constraint Programming System (not to be confused with the Eclipse IDE) can be embedded and called from C / C++ and has an interface for C / C++, Python, Java, and even PHP. The various Prolog implementations also often have a C / C++ interface.
There are also many libraries available that add constraint programming features to traditionally imperative programming languages. For users of C/C++, there are Gecode, Minion and Comet. For Java developers there are Choco and Cream. For Python, you have Python-constraint and Numberjack. There is also a multi-language constraint programming library by Google called or-tool that supports C++, Python, Java and .NET.
There are many domains and paradigms of programming that can make certain kinds of programs much simpler to develop. Now that you have some knowledge of constraint programming in your vocabulary to pull out whenever needed, hopefully you will explore and find out more.